Diode Bandgap 1.12V (fait maison)
SOURCE DE TENSION DE REFERENCE
Dans les techniques de mesure et de régulation, l'usage de tensions de références est très répandu, puisque l'action de mesurer consiste à comparer une grandeur inconnue à une grandeur Un des problèmes qui se posent est celui de la plus ou moins grande instabilité de la référence. la température, le courant de charge et la tension d'alimentation. La diode zener (cf. figure 1) est utilisable à condition que ni la température, ni le courant de charge, ni la tension d'alimentation ne varient trop fortement. |
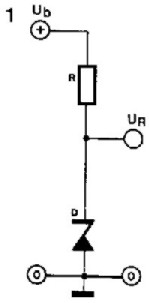 |
La solution de la figure 2 est généralement préférable. Reste le coefficient thermique que l'on pourrait chercher à améliorer. Les électrons qui se trouvent au niveau énergétique le plus élevé contribuent à la conduction. A mesure qu'augmente température du matériau, le nombre d'électrons susceptibles de franchir la bande interdite augmente aussi : Pour que le circuit fonctionne bien, il faut que la valeur de R2 soit à peut près 10 fois supérieure à celle de R1, et que celle R3 soit établie de telle sorte que UR soit de 1.204V, enfin que les deux transistors soient parfaitement identiques (cette dernière condition ne peut être remplie qu'en faisant appel à des transistors d'u même puce (par exemple des réseaux de transistors comme le CA3086). La valeur de la résistance R à déterminer en fonction de la tension d'alimentation et du courant de sortie maximal. Il ne faut pas perdre de vue qu'à vide, ce courant circule à travers T3, ce qui va se traduire par des variations de température dues à la dissipation de puissance dans T3. Il est donc préférable de ne pas laisser ce type source de tension de référence hors charge. Un avantage supplémentaire d'un circuit comme celui-ci est qu'il se contente d'une tension d'alimentation de 1.5V seulement. Dans le cadre ci-contre apparaît la démonstration de la stabilité thermique de cette source de tension de référence. |
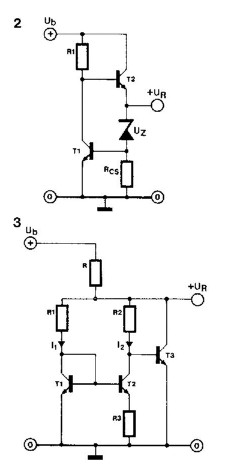 |
Lorsque le gain du transistor T2 est suffisant, la quasi totalité de i2 circule à travers R3 :
| k = constante de Boltzmann (1.3805*10e-23 J/°K) |
| UBE = UBG(1-T/To) + UBEo(T/To) ( η aproximaivement 1.5 pour un transistor double diffusion) |
| en référence à l'équation, les deux dernières limites sont tout à fait petites et sont rendues plus petit encore en faisant l'ic changent en tant que température absolue. en tout cas, elles peuvent être ignorées pour maintenant parce qu'elles sont du même ordre que des erreurs provoquées par le comportement nontheoretical des transistors qui doivent être déterminés empiriquement |
| referring to equation, the last two terms are quite small and are made even smaller by making ic vary as absolute temperature. at any rate, they can be ignored for now because they are of the same order as errors caused by nontheoretical behavior of transistors that must be determined empirically |
UBE1 = UBG(1-T/To) + UBE1o(T/To)
UBE2 = UBG(1-T/To) + UBE2o(T/To)
et comme UBE1o = UBE2o et iC1o = iC2o
UBE(T1) - UBE(T2) = σ * Ln( i1 / i2 )
dUR/dT = (QFD)
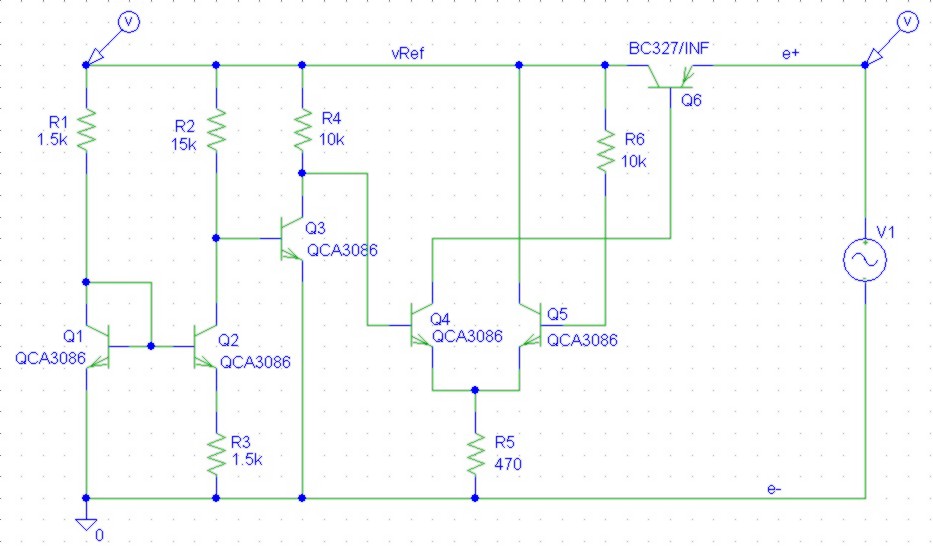
|
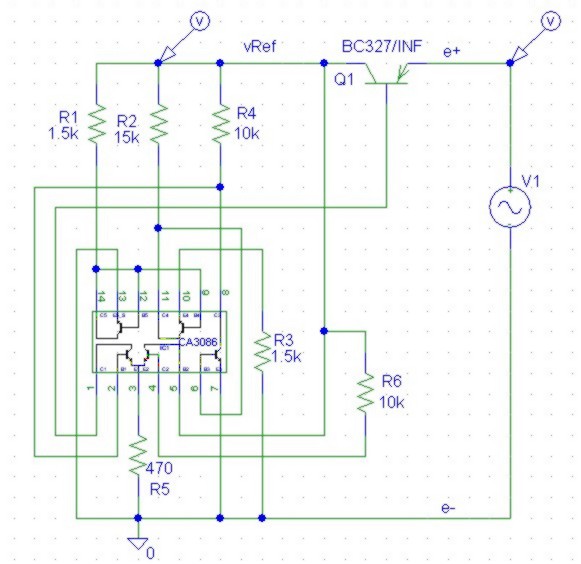 |
|
P.S :
Résultat : (Alimentation fixe de 1,21V)
****************************************************
* Bandgap 1.12V .MODEL BC327 PNP (IS=0.230P NF=1.000 BF=504.327 VAF=26.000 IKF=0.780 .SUBCKT Bandgap_1-12V e+ e- vRef R1 vRef 109 1.5k
Q1 101 102 103 e- QCA3086 |


Réglages :
Avec PSpice d'Orcad
** Analysis setup **
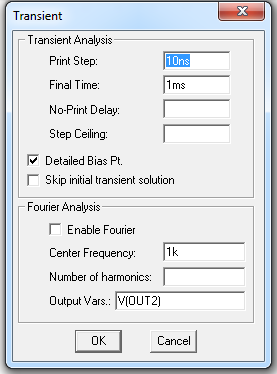
.tran/OP 10ns 1ms
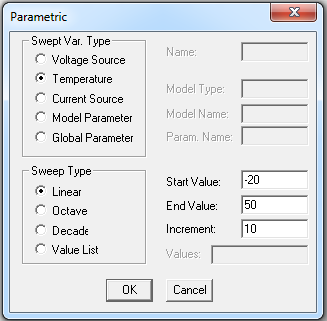
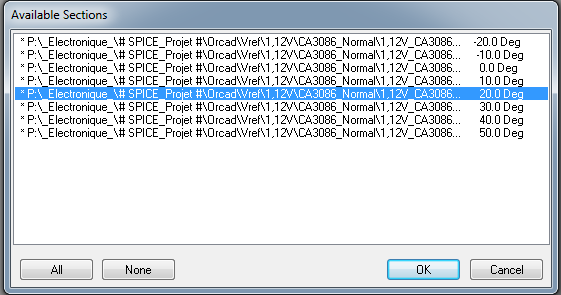
.STEP LIN TEMP -20 50 10
.OP
Résultats :
Alimentation Minimum, environs 1,21V avans répercution sur la régulation :
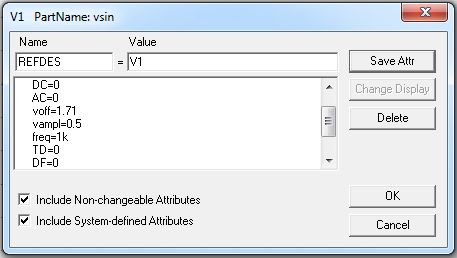
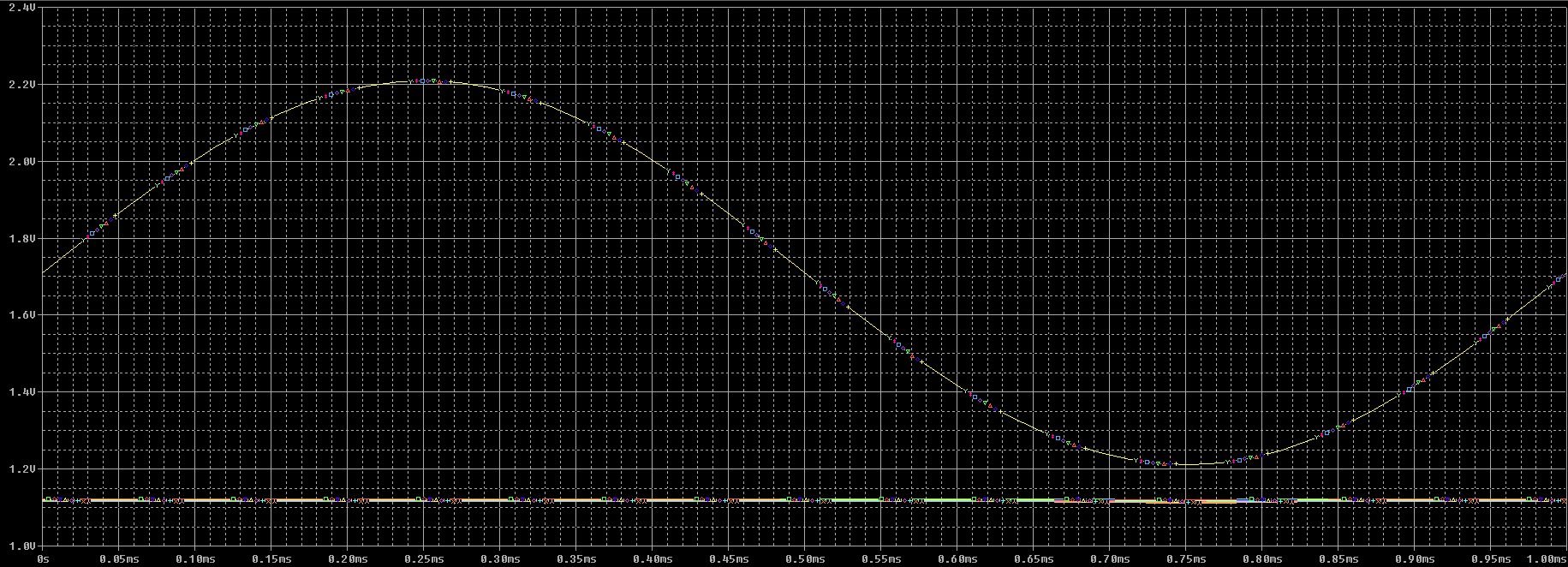
Réglage des paramettre de V1 pour que 1,21V < V1 < 2,21V :
Amplitude des variations du au températures (pour V1 à 1,21V ):
1,12088V à -20°C
1,112V à +50°C
Soit environs 8,88mV de variation pour une variation de plage de température de -20°C à +50°C
Soit -0,127mV / °C
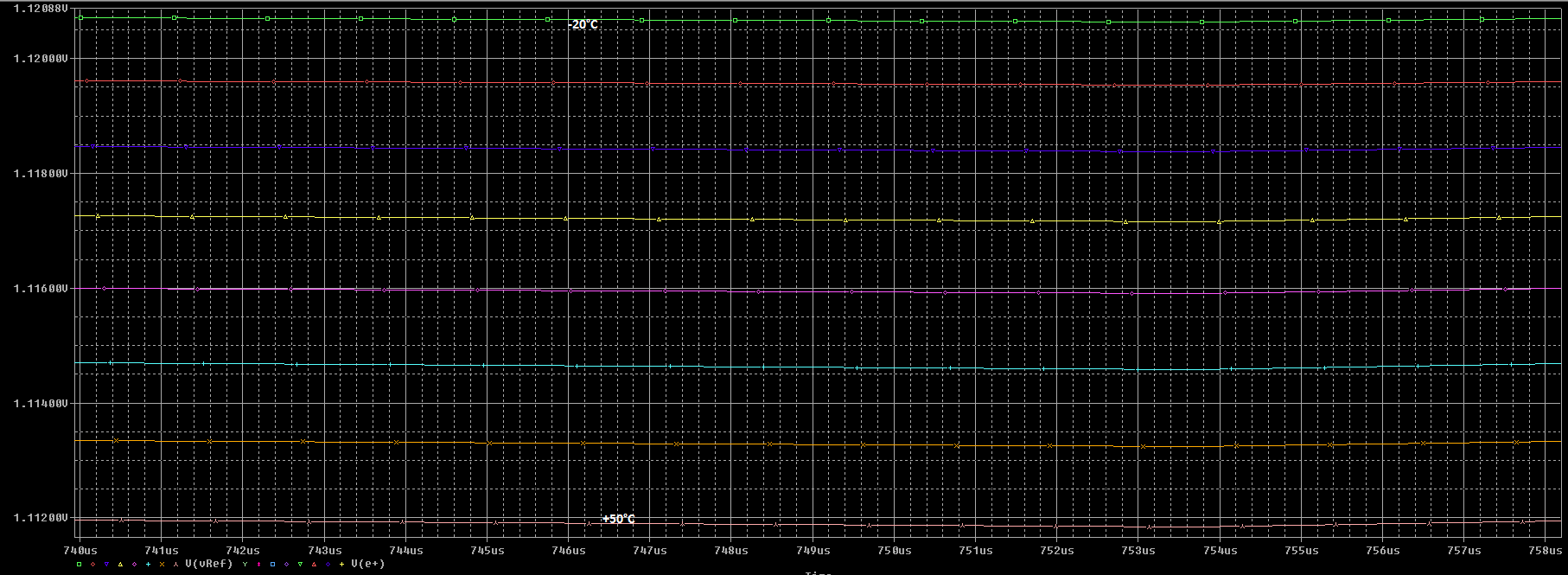
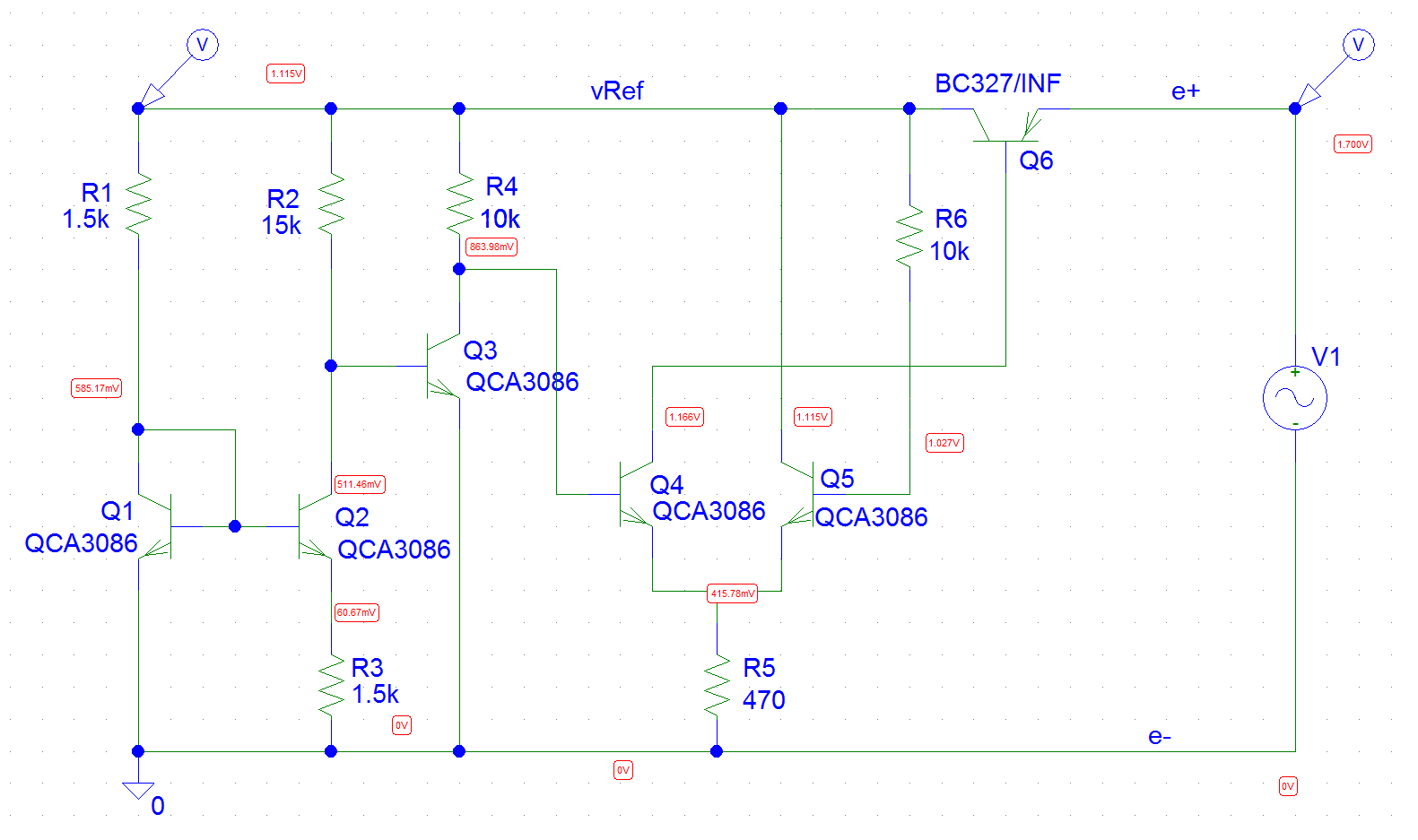
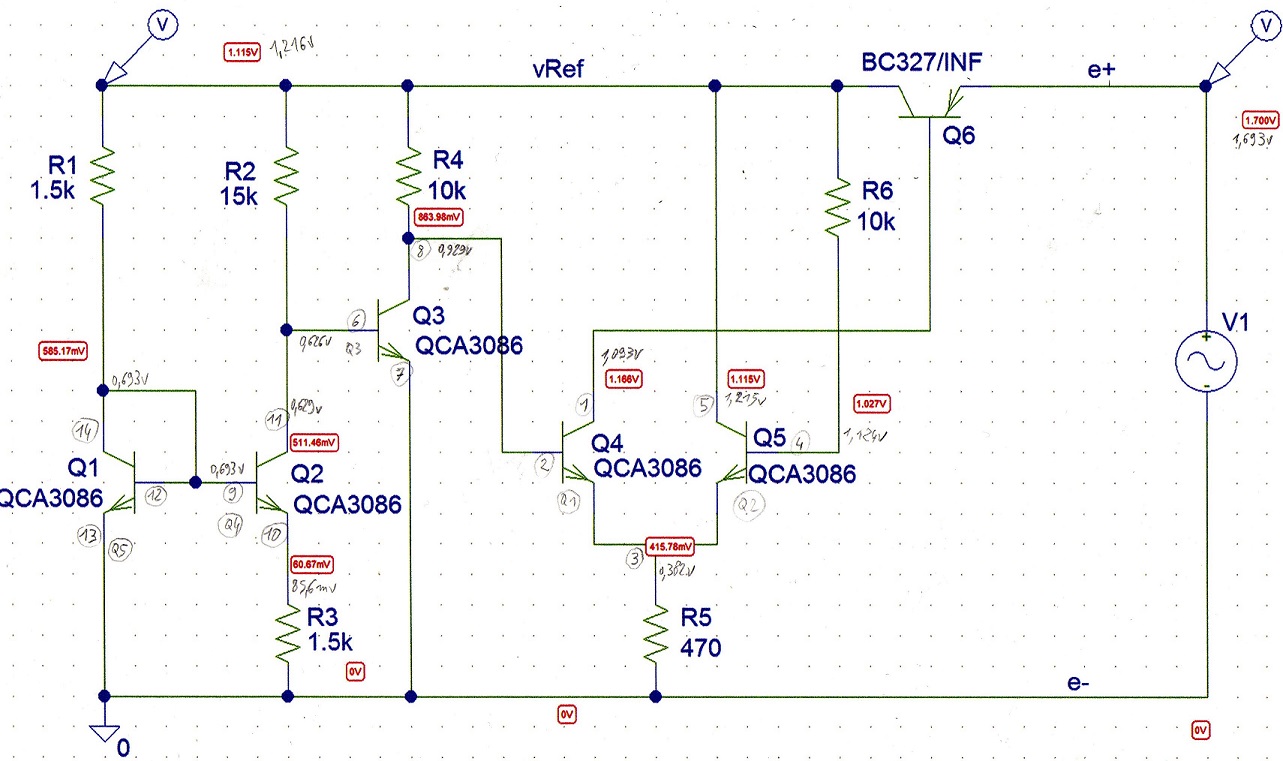
Schéma avec Voltages en statique pour alimentation 1.7V :
Test avec LTspice :
1-12V_BandGap.asc (Fichier LTspice du schéma)
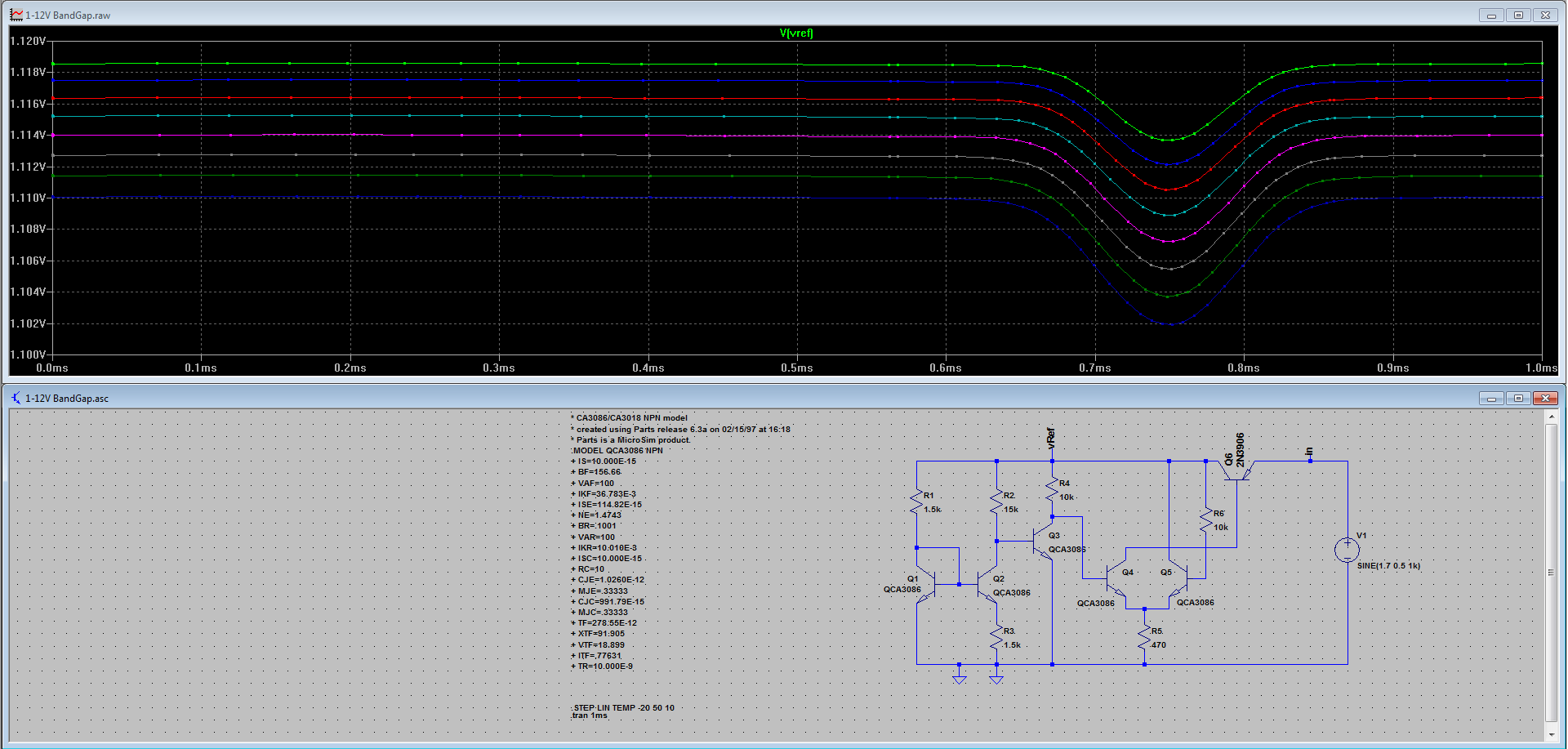
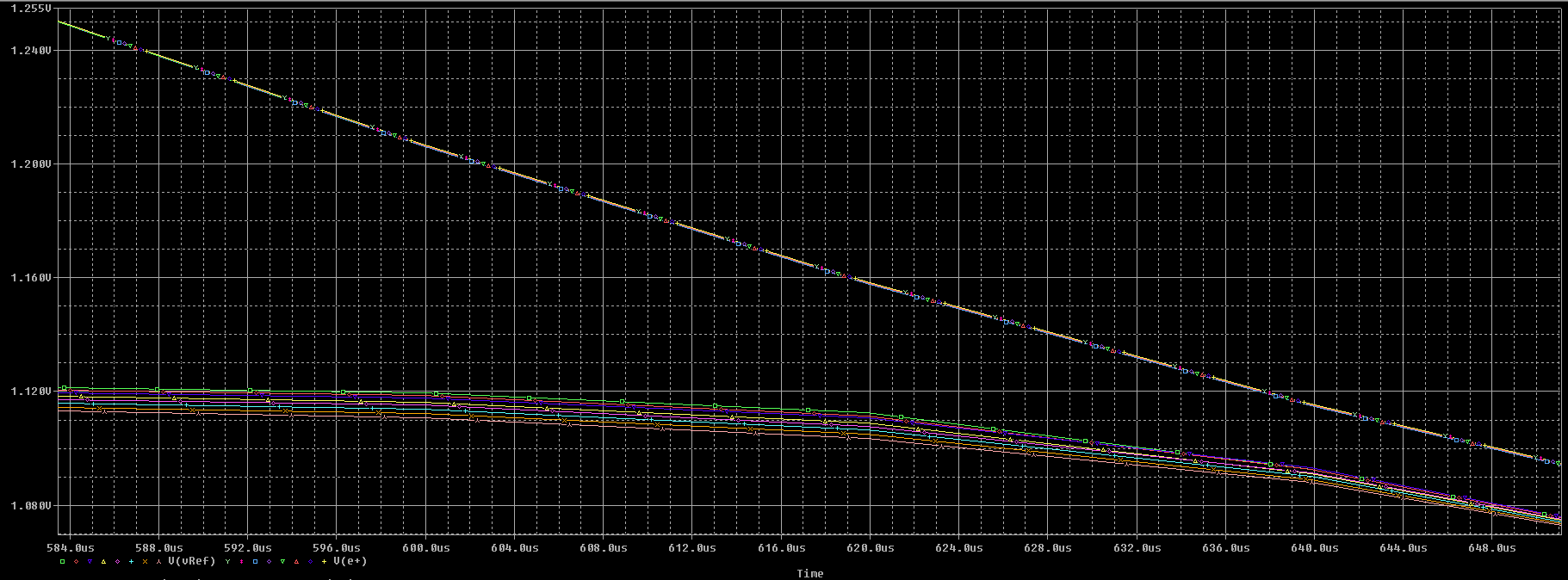
On remarque que sous LTspice pour le Voltage Vin le plus bas, la tension Vref n'est plus stable.
Il y as donc des différences de simulation entre Orcad Pspice et LTspice.
Si on reste avec une alimentation de l'ordre de 1.7V début du graphique nous avont :
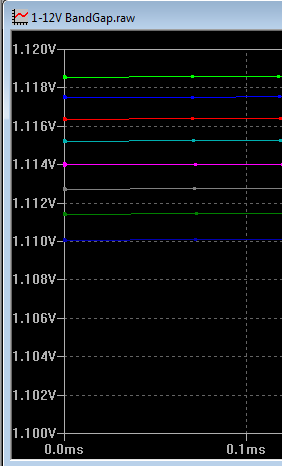
En vert c'est pour -20°C (en haut) : 1.119V
En bleu foncé pour +50°C (en bas) : 1.11V
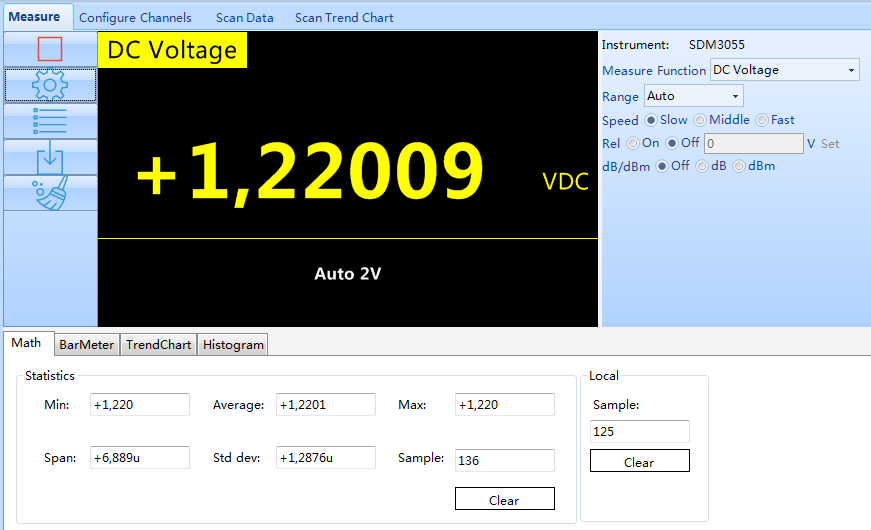
un petit essai avec mon générateur de fonction : 3VDC + sinus 1V à 1kHz ça reste bien à 1.22V
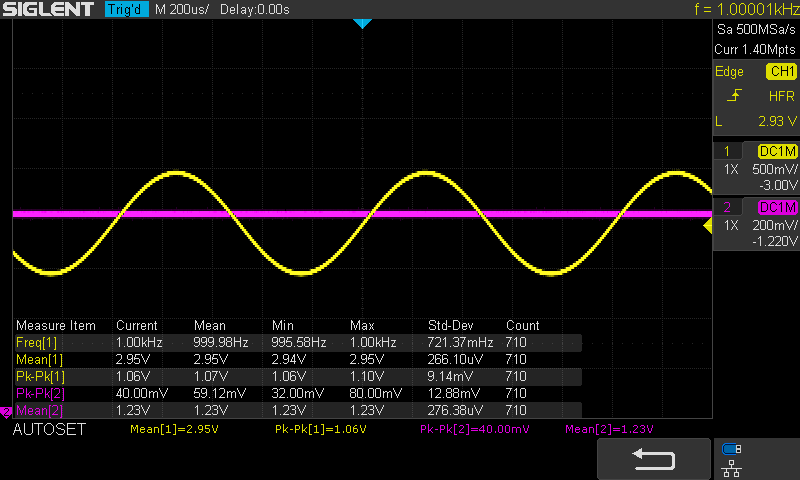
mesure avec le SDM3055 :
Fichiers Eagle :
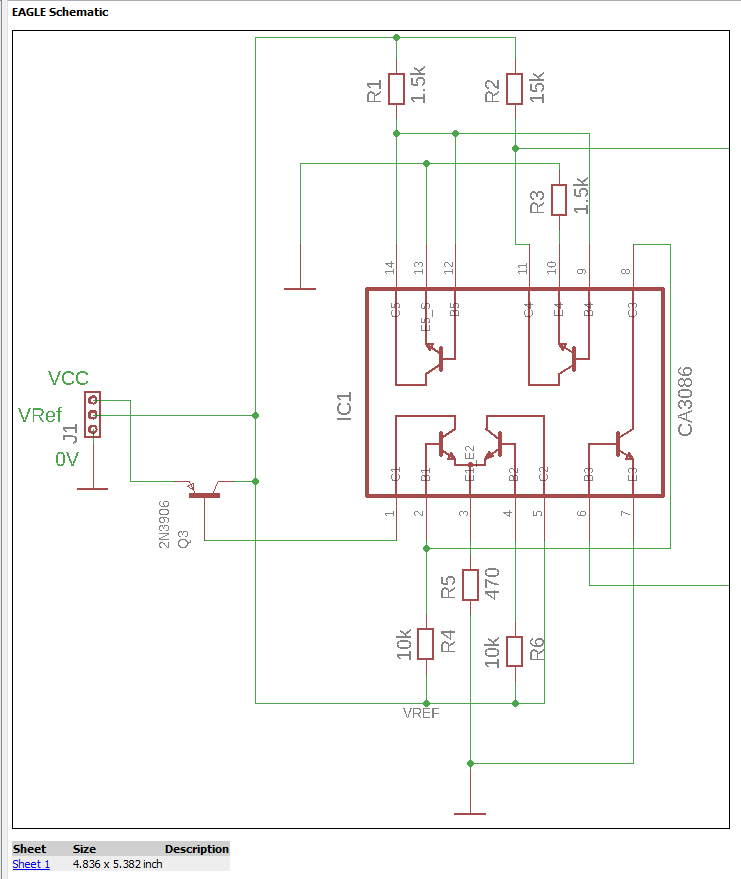
BANDGAP.SCH (Fichier schéma Eagle)
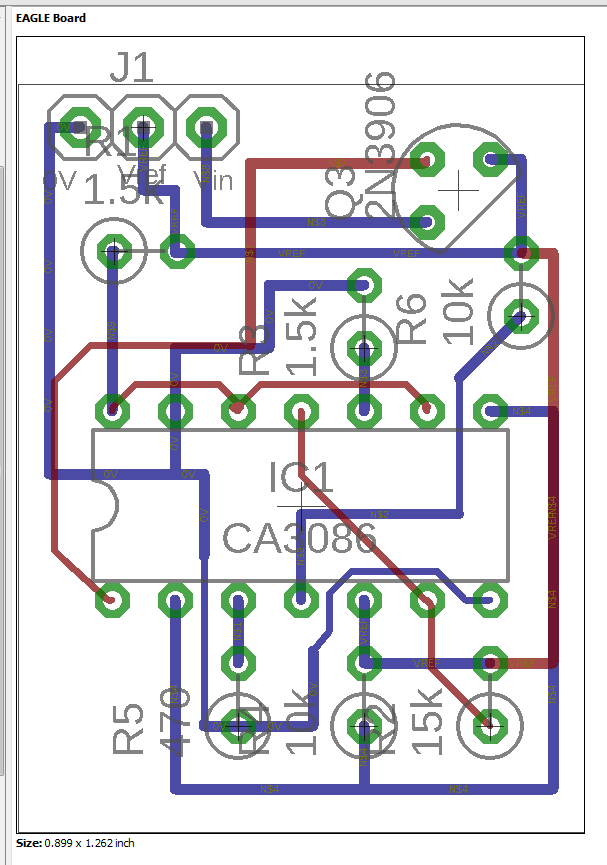
BANDGAP.BRD (Fichier circuit imprimé Eagle)
Retour électronique